Анализ Газпрома от Миколы (известного аналитика и стратега)
Что, если те, за кем наблюдает Vanutar, сами ничего не понимают? Странная нефрактальность.
Фрактальность рынка — практические наблюдения.
(Для тех, кому внове фрактальная модель: о ней можно прочитать, например, в
старых блогах Миколы. А вообще Мандельброт придумал фракталы именно наблюдая
за рынком. Данный блог предполагает, что читатель знаком с фрактальной моделью)
Резюме: линейный рост рынка, регулярно наблюдающийся последние пару лет
на таймфреймах дни-недели, — очень странное явление.
1. Он никак не сочетается с фрактальной моделью рынка (а фрактальная модель,
если вдуматься, наиболее естественная базовая модель рынка — и одна из немногих
моделей, грамотно енкапсулирующих авторефлексивность).
2. Он говорит о том, что сообщество среднесрочных спекулянтов неверно
оценивает рынок, и видимо, не зарабатывает денег.
3. Что вызывает вопросы о том, содержит ли их поведение информацию о будущем
движении рынка — если они начисто не умеют предсказать рынок, что пользы в
наблюдении за ними?
Сначала уточним такую деталь: единственным источником денег для среднесрочных
спекулянтов являются деньги более медленных таймфреймов. Т.е. понятно, что
среднесрочные спеки могут переигрывать друг друга, но это игра с нулевой
суммой. Как сообщество они могут зарабатывать только на том, чтобы угадать
начало притока медленных денег и стремительно задрать цену, чтобы медленные
деньги купили у них дорого. (Или, соответственно, угадать начало оттока и
заранее обрушить цену).
Поэтому график индекса может, грубо говоря, выглядеть либо
1. Как броуновское движение — типичная фрактальная картинка — в отсутствии
существенного притока/оттока денег
или
2. Как быстрое движение к новому уровню с последующей релаксацией — если рынок
почуял начало притока/оттока.
Линейный рост означает, что идёт постоянный приток медленных денег, а среднесрочные
спекулянты не самоорганизовались, не вычислили начало притока, не задрали
цену заранее и продолжают бессмысленно и разобщённо метаться — нет вообще
никаких следов самоорганизации (если бы она была, то были бы коррекции и взлёты — линейный график говорит о том, что самоорганизации нет).
Задача технического анализа в том, чтобы на основе прошлого графика предсказать
будущий, говорит определение. Подход в том, чтобы увидеть, что делают крупные игроки
(по контексту понятно, что речь идёт в первую очередь об игроках среднего таймфрейма),
говорит Иван Vanutar. Всё это здорово, но что делать, если график показывает
только, что среднесрочные игроки ни хрена не понимают и (в целом, как группа) сидят
в минусах?
Если дерево обросло мхом со всех сторон — это что, значит Северный Полюс — сверху?
Т.е. стоит ли искать новый подход — такую авторефлексивную модель рынка, в которой
линейные участки будут естественно возникать, или просто решить, что существующие
модели адекватно всё описывают — и странности графика объясняются тем, что среднесрочные спеки не рубят фишку — и никакой моделью этот странный факт не изменить?
Иными словами, несоответствие рынка нашим подходам — это повод сказать, что
рынок неправильный, или стоит поискать новый подход?
И да, кстати. Есть знаменитый спор о гипотезе эффективного рынка — насколько она верна.
Вот судя по распространённости линейных учасков графика, ни хрена не верна.

(Для тех, кому внове фрактальная модель: о ней можно прочитать, например, в
старых блогах Миколы. А вообще Мандельброт придумал фракталы именно наблюдая
за рынком. Данный блог предполагает, что читатель знаком с фрактальной моделью)
Резюме: линейный рост рынка, регулярно наблюдающийся последние пару лет
на таймфреймах дни-недели, — очень странное явление.
1. Он никак не сочетается с фрактальной моделью рынка (а фрактальная модель,
если вдуматься, наиболее естественная базовая модель рынка — и одна из немногих
моделей, грамотно енкапсулирующих авторефлексивность).
2. Он говорит о том, что сообщество среднесрочных спекулянтов неверно
оценивает рынок, и видимо, не зарабатывает денег.
3. Что вызывает вопросы о том, содержит ли их поведение информацию о будущем
движении рынка — если они начисто не умеют предсказать рынок, что пользы в
наблюдении за ними?
Сначала уточним такую деталь: единственным источником денег для среднесрочных
спекулянтов являются деньги более медленных таймфреймов. Т.е. понятно, что
среднесрочные спеки могут переигрывать друг друга, но это игра с нулевой
суммой. Как сообщество они могут зарабатывать только на том, чтобы угадать
начало притока медленных денег и стремительно задрать цену, чтобы медленные
деньги купили у них дорого. (Или, соответственно, угадать начало оттока и
заранее обрушить цену).
Поэтому график индекса может, грубо говоря, выглядеть либо
1. Как броуновское движение — типичная фрактальная картинка — в отсутствии
существенного притока/оттока денег
или
2. Как быстрое движение к новому уровню с последующей релаксацией — если рынок
почуял начало притока/оттока.
Линейный рост означает, что идёт постоянный приток медленных денег, а среднесрочные
спекулянты не самоорганизовались, не вычислили начало притока, не задрали
цену заранее и продолжают бессмысленно и разобщённо метаться — нет вообще
никаких следов самоорганизации (если бы она была, то были бы коррекции и взлёты — линейный график говорит о том, что самоорганизации нет).
Задача технического анализа в том, чтобы на основе прошлого графика предсказать
будущий, говорит определение. Подход в том, чтобы увидеть, что делают крупные игроки
(по контексту понятно, что речь идёт в первую очередь об игроках среднего таймфрейма),
говорит Иван Vanutar. Всё это здорово, но что делать, если график показывает
только, что среднесрочные игроки ни хрена не понимают и (в целом, как группа) сидят
в минусах?
Если дерево обросло мхом со всех сторон — это что, значит Северный Полюс — сверху?
Т.е. стоит ли искать новый подход — такую авторефлексивную модель рынка, в которой
линейные участки будут естественно возникать, или просто решить, что существующие
модели адекватно всё описывают — и странности графика объясняются тем, что среднесрочные спеки не рубят фишку — и никакой моделью этот странный факт не изменить?
Иными словами, несоответствие рынка нашим подходам — это повод сказать, что
рынок неправильный, или стоит поискать новый подход?
И да, кстати. Есть знаменитый спор о гипотезе эффективного рынка — насколько она верна.
Вот судя по распространённости линейных учасков графика, ни хрена не верна.

Как «на глаз» определить лажу аналитика.
Продолжу, потихоньку спасать с хумона свое добро, нажитое непосильным трудом! :)))
Ни для кого не секрет, что аналитики частенько «лажают» в своих прогнозах. Иногда это происходит по незнанию или ошибке, иногда намеренно. Отличить откровенную лажу от правдоподобного и честного анализа часто довольно сложно. Для этого нужен достаточно большой объем специальных знаний и/или большой опыт.
Есть, однако, один случай, когда лажу можно определить достаточно легко. Речь идет о прогнозах ценовых уровней, который рынок достигнет за то или иное время. Это когда мы слышим, например, в программе РБК слова «эксперта» о том, что «мы ждем индекс ММВБ на уровне 3000 до конца года». Или когда «уважаемая» компания пишет, что «акции Газпрома вполне могут достичь 250 к середине лета». Или когда комментаторы в лентах соцсетей твердят, что «завтра ММВБ будет штурмовать 800». Вот в таких случаях есть способ легко понять кто перед нами – серьезный человек, или лох, а то и того хуже – откровенный манипулятор, целью которого является создание определенного мнения в инвестиционном сообществе.
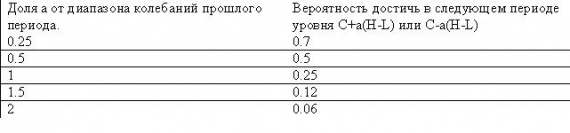
Дело вот в чем. Все финансовые рынки, связанные с плохо определенными рисками (акции, валюты, фьючерсы) обладают одним простым и интересным свойством: Вероятность того, что диапазон колебаний за какой-то будущий период (час, день, неделя, месяц, год) будет больше диапазона колебаний такого же периода в прошлом около 0,5. Например, если сегодня акции Газпрома колебались на 3 рубля в течение дня (разность между максимумом и минимумом сегодняшнего дня), то завтра диапазон их колебаний будет больше 3 рублей с вероятностью 0,5. Больший диапазон колебаний менее вероятен. Меньший диапазон колебаний более вероятен. Скажем, вероятность колебаний на 1 рубль будет около 90 %, а вероятность колебаний на 5 рублей будет всего около 15 %.
Когда-то давно я довольно долго занимался свойствами волатильности, и ее частного случая – диапазонов колебаний цен за заданный период времени. Они довольно сложны и интересны, повторяются (являются инвариантными) на достаточно большом диапазоне масштабов (примерно от минут до года), позволяют получать интересные прогнозы. Но для простейших прикидок, в частности, я вывел упрощенную зависимость для вероятности достижения завтра (или в течение недели, месяца, года – на любом заданном заранее интервале времени) каких либо уровней. Простейшее правило здесь такое: максимум следующего периода будет выше закрытия на половину диапазона колебаний прошлого периода с вероятностью 0,5. И минимум следующего периода будет ниже закрытия на половину диапазона колебаний прошлого периода с вероятностью 0,5.
Для знакомых с математикой: общая приблизительная формула расчета вероятности достижения уровня:
P(C(i)+a*(H(i)-L(i))=exp(-1.4*a)
Или русским языком: Вероятность преодолеть уровень, который лежит выше/ниже закрытия на долю а от диапазона прошлых колебаний равна экспоненте в степени -1,4*а.
(Небольшой комментарий, который большинство может пропустить, но для зануд, хорошо знакомых с предметом: данная формула достаточно хорошо описывает искомую зависимость в диапазоне вероятностей от примерно 0,05 до 0,85 чего вполне достаточно для большинства житейских рыночных ситуаций. В области малых вероятностей (редких событий) действует другой закон, как правило степенной и приведенная формула сильно занижает искомые вероятности, в области высоких вероятностей также надо искать другую закономерность и приведенная формула завышает вероятности. Кроме того, если за прошлый период произошло сильное увеличение или уменьшение амплитуды колебаний (более чем в два раза по отношению к позапрошлому периоду), то эта формула так же будет давать ошибочные значения. В этих случаях необходимо вводить поправки, либо использовать средний диапазон колебаний за несколько прошлых периодов).
Для тех кому лениво или сложно считать экспоненты дам простую таблицу, с помощью которой можно легко определять эти вероятности:
Как пользоваться таблицей.
Возьму пример из моего январского прогноза, а именно прогноз возможных годовых уровней для индекса ММВБ.
В 2012 году необходимые значения индекса ММВБ составили:
Максимум 1639
Минимум 1241
Закрытие 1477
Диапазон колебаний 1639 – 1241=398
Уровни, которых в 2013 году индекс может достичь вверху:
1477+0,5*398=1676 с вероятностью 50 %
1477+1*398=1875 с вероятность 25 %
1477+1,5*398=2074 с вероятностью 12 %
Уровни, которых в 2013 году индекс может достичь внизу:
1477-0,5*398=1278 с вероятностью 50 %
1477-1*398=1079 с вероятность 25 %
1477-1,5*398=880 с вероятностью 12 %
На всякий случай, предупреждение. И формула и таблица являются приближенными и могут быть использованы только для первой, грубой оценки шансов достижения тех или иных уровней. Ни в коем случае не используйте их в приведенном виде для принятия торговых решений! Вероятность – штука хитрая. Достижение ценой уровня, вероятность которого мала, ни в коем случае не означает, что цена развернется от этого уровня и пойдет обратно!
Можно использовать этот метод, например, для оценки рисков открытой позиции. Зная уровни снизу и вероятности их достижения можно оценить размер и вероятность возможных убытков длинной позиции. Для короткой позиции можно оценить размер и вероятность убытков по уровням сверху.
А слушая и читая аналитиков, можно даже «на глаз» определять правдоподобность их прогнозов: если человек говорит о высоких вероятностях достижения целей, которые лежит выше/ниже 1-2 размера колебаний за прошлый период, то перед нами либо лох, ничего не знающий о рынке, либо мошенник и манипулятор, а вероятность исполнения его «прогноза» существенно меньше 50 %.
Ни для кого не секрет, что аналитики частенько «лажают» в своих прогнозах. Иногда это происходит по незнанию или ошибке, иногда намеренно. Отличить откровенную лажу от правдоподобного и честного анализа часто довольно сложно. Для этого нужен достаточно большой объем специальных знаний и/или большой опыт.
Есть, однако, один случай, когда лажу можно определить достаточно легко. Речь идет о прогнозах ценовых уровней, который рынок достигнет за то или иное время. Это когда мы слышим, например, в программе РБК слова «эксперта» о том, что «мы ждем индекс ММВБ на уровне 3000 до конца года». Или когда «уважаемая» компания пишет, что «акции Газпрома вполне могут достичь 250 к середине лета». Или когда комментаторы в лентах соцсетей твердят, что «завтра ММВБ будет штурмовать 800». Вот в таких случаях есть способ легко понять кто перед нами – серьезный человек, или лох, а то и того хуже – откровенный манипулятор, целью которого является создание определенного мнения в инвестиционном сообществе.
Дело вот в чем. Все финансовые рынки, связанные с плохо определенными рисками (акции, валюты, фьючерсы) обладают одним простым и интересным свойством: Вероятность того, что диапазон колебаний за какой-то будущий период (час, день, неделя, месяц, год) будет больше диапазона колебаний такого же периода в прошлом около 0,5. Например, если сегодня акции Газпрома колебались на 3 рубля в течение дня (разность между максимумом и минимумом сегодняшнего дня), то завтра диапазон их колебаний будет больше 3 рублей с вероятностью 0,5. Больший диапазон колебаний менее вероятен. Меньший диапазон колебаний более вероятен. Скажем, вероятность колебаний на 1 рубль будет около 90 %, а вероятность колебаний на 5 рублей будет всего около 15 %.
Когда-то давно я довольно долго занимался свойствами волатильности, и ее частного случая – диапазонов колебаний цен за заданный период времени. Они довольно сложны и интересны, повторяются (являются инвариантными) на достаточно большом диапазоне масштабов (примерно от минут до года), позволяют получать интересные прогнозы. Но для простейших прикидок, в частности, я вывел упрощенную зависимость для вероятности достижения завтра (или в течение недели, месяца, года – на любом заданном заранее интервале времени) каких либо уровней. Простейшее правило здесь такое: максимум следующего периода будет выше закрытия на половину диапазона колебаний прошлого периода с вероятностью 0,5. И минимум следующего периода будет ниже закрытия на половину диапазона колебаний прошлого периода с вероятностью 0,5.
Для знакомых с математикой: общая приблизительная формула расчета вероятности достижения уровня:
P(C(i)+a*(H(i)-L(i))=exp(-1.4*a)
Или русским языком: Вероятность преодолеть уровень, который лежит выше/ниже закрытия на долю а от диапазона прошлых колебаний равна экспоненте в степени -1,4*а.
(Небольшой комментарий, который большинство может пропустить, но для зануд, хорошо знакомых с предметом: данная формула достаточно хорошо описывает искомую зависимость в диапазоне вероятностей от примерно 0,05 до 0,85 чего вполне достаточно для большинства житейских рыночных ситуаций. В области малых вероятностей (редких событий) действует другой закон, как правило степенной и приведенная формула сильно занижает искомые вероятности, в области высоких вероятностей также надо искать другую закономерность и приведенная формула завышает вероятности. Кроме того, если за прошлый период произошло сильное увеличение или уменьшение амплитуды колебаний (более чем в два раза по отношению к позапрошлому периоду), то эта формула так же будет давать ошибочные значения. В этих случаях необходимо вводить поправки, либо использовать средний диапазон колебаний за несколько прошлых периодов).
Для тех кому лениво или сложно считать экспоненты дам простую таблицу, с помощью которой можно легко определять эти вероятности:

Как пользоваться таблицей.
Возьму пример из моего январского прогноза, а именно прогноз возможных годовых уровней для индекса ММВБ.
В 2012 году необходимые значения индекса ММВБ составили:
Максимум 1639
Минимум 1241
Закрытие 1477
Диапазон колебаний 1639 – 1241=398
Уровни, которых в 2013 году индекс может достичь вверху:
1477+0,5*398=1676 с вероятностью 50 %
1477+1*398=1875 с вероятность 25 %
1477+1,5*398=2074 с вероятностью 12 %
Уровни, которых в 2013 году индекс может достичь внизу:
1477-0,5*398=1278 с вероятностью 50 %
1477-1*398=1079 с вероятность 25 %
1477-1,5*398=880 с вероятностью 12 %
На всякий случай, предупреждение. И формула и таблица являются приближенными и могут быть использованы только для первой, грубой оценки шансов достижения тех или иных уровней. Ни в коем случае не используйте их в приведенном виде для принятия торговых решений! Вероятность – штука хитрая. Достижение ценой уровня, вероятность которого мала, ни в коем случае не означает, что цена развернется от этого уровня и пойдет обратно!
Можно использовать этот метод, например, для оценки рисков открытой позиции. Зная уровни снизу и вероятности их достижения можно оценить размер и вероятность возможных убытков длинной позиции. Для короткой позиции можно оценить размер и вероятность убытков по уровням сверху.
А слушая и читая аналитиков, можно даже «на глаз» определять правдоподобность их прогнозов: если человек говорит о высоких вероятностях достижения целей, которые лежит выше/ниже 1-2 размера колебаний за прошлый период, то перед нами либо лох, ничего не знающий о рынке, либо мошенник и манипулятор, а вероятность исполнения его «прогноза» существенно меньше 50 %.
Мифы и реальность фигур технического анализа.
Продолжаю спасение своих утопающих на комоне блогов. Сегодня наткнулся на старый текст, но актуальности нифига не потерявший.
В конце девятнадцатого века, примерно в одно и тоже время, появились две совершенно противоположные по смыслу концепции, описывающие поведение цен на фондовом рынке. В 1900-м году Луи Башелье написал диссертацию «теория спекуляций», основанную на наблюдениях за поведением цен облигаций на парижской бирже. За семь лет до Эйнштейна он предложил формальную математическую модель случайного блуждания, в соответствии с которой поведение цен было похоже на поведение броуновской частицы под ударами мелких молекул.
В период с 1890 по 1902 годы Чарльз Доу, первый редактор газеты «Wall Street Journal» и автор самого известного биржевого индекса, написал серию статей, которая позже превратилась в «теорию Доу». Он считал, что поведение цен описывается закономерными тенденциями, или направленными движениями вверх или вниз, которые отражают господствующее на бирже мнение о будущем экономики или отдельной компании. Так началось противостояние двух принципиально противоположных концепций, которое не окончено и по сей день.
Гипотеза Башелье за период с 1930 по 1950-й годы превратилась в гипотезу эффективного рынка, на котором большое количество независимых рациональных участников быстро и правильно принимают решения на основе поступающей информацию. В результате вся имеющаяся на рынке информация оказывается включенной в цену, а поведение цен оказывается случайным блуждание, которое невозможно прогнозировать. Эта теория господствовала в академической теории финансов вплоть до конца двадцатого века.
Теория Доу пришлась больше по нраву трейдерам, реально торгующим на фондовом рынке, поскольку позволяла принимать решения на основе анализа ценовых графиков, что с точки зрения гипотезы эффективного рынка делать бессмысленно – все видимые глазом движения цен являются «причудливой игрой случая», как выпадение красного или черного в рулетке. Однако, практики знали, что это не так, или по крайней мере не совсем так. Уже в тридцатых годах двадцатого века, на основе положений Чарльза Доу была разработана классификация «типичных» вариантов поведения цен, означающих смену или продолжение наблюдаемой рыночной тенденции. Сейчас их называют «фигурами» или паттернами, а обнаружение таких фигур на графиках техническим визуальным анализом. В отличие от индикаторного технического анализа, требующего иногда достаточно сложных расчетов, визуальный анализ весьма прост – для него необходимо только видеть график цены и помнить наиболее важные фигуры.
Между тем даже сегодня фигуры технического анализа остаются одной из наиболее спорных тем. С одной стороны, их видит на графиках практически любой начинающий трейдер. С другой стороны, работа фигур теханализа по правилам, описанных в книгах, вызывает большие сомнения, особенно когда начинается «проверка гармонии алгеброй», т.е. формальные и статистически правильные исследования. Если рассматривать паттерны типа «голова и плечи» и т.д. отвлеченно от рынка, как некие образы, картинки, возникающие в графиках цены, то грамотная статистическая проверка будет неизменно приводить к печальному результату: вероятность срабатывания фигуры по сценарию, описанному в книгах близка к 50 %. Однако, иногда они срабатывают очень даже хорошо. Можно ли отличить ситуацию когда фигура сработает, от обратной? Иногда можно.
Но для того, чтобы ответить на вопрос о срабатывании фигур сначала нужно ответить на более фундаментальный вопрос: что движет рынком?
Один из возможных, достаточно очевидных ответов – решения участников рынка, реализованные в сделках. Почему люди принимают решения? Достаточно очевидный ответ, в духе академической науки — реагируя на информацию. Следовательно, одним из важных факторов движения цен является информация, поступающая на рынок. Ее можно разделить на четыре категории:
Очевидно положительная – такая информация, которая для большинства участников рынка является понятным поводом для покупки.
Очевидно отрицательная – такая, которая для большинства участников является основанием для продажи.
Нейтральная – это весьма частый вид информации (пожалуй, наиболее частый на рынке), когда ее можно интерпретировать и как положительную и как отрицательную. Эта информация вызывает у части участников решения о покупке, а у другой части – решения о продаже.
И наконец, есть еще один вид информации – ее отсутствие. Это периоды на рынке, когда выходящие новости настолько слабы, что не вызывают реакции участников рынка в виде сделок.
Согласно современным представлениям, поступление информации на рынок — процесс близкий к случайному (математики говорят пуассоновский). Да, конечно, бывают периоды, когда одна за другой долго идут положительные или отрицательные новости, но такие периоды редки. Поэтому, если бы движение определялось только информацией, то цены были бы в точности случайным блужданием, как это и предполагает гипотеза эффективного рынка.
Однако, есть еще один фактор, который на сегодня можно считать доказанным и который вносит коррективы в движение цен. Это настроения участников рынка, определяющие их отношение к информации. Численным выразителем настроений участников может быть фрактальная размерность графика цены, или является знаменитый показатель Херста H, связанный с фрактальной размерностью соотношением D=2-H. Его значение задает три возможных типа поведения участников рынка, которые можно описать так.
При H>0.5 настроения «кооперативны» и участники склонны одинаково оценивать выходящие новости. В первом приближении значение Н задает вероятность, с которой участники принимают одинаковые решения на основе выходящей информации. Такое состояние обычно связывается с трендами, поскольку движение цены вверх (вниз) вызывает еще большее желание рыночной толпы покупать (продавать) акции.
Если Н близко к 0.5, то участники рынка склонны действовать независимо друг от друга, независимо оценивать информацию и независимо принимать решения. Поведение цены в данном случае — это классическое случайное блуждание.
При Н<0.5, то участники рынка склонны к антикооперативному поведению. Грубо говоря, они склонны трактовать выходящие новости и движения цен «наоборот». В таком состоянии движение цены вверх вызывает желание продавать акции, а вниз – наборот покупать их. Такое поведение характерно для флэтов.
Таким образом, четыре типа информации три типа поведения участников задают нам все встречающие рыночные ситуации. Поведение цен в этих ситуациях склонно к формированию неких «типичных» паттернов, которые являются отражением преобладающей на рынке информации и характера реакции участников рынка на эту информацию. Вот эти типичные паттерны поведения цен в различных информационно-настроенческих ситуациях с моей точки зрения и составляют набор фигур технического анализа:
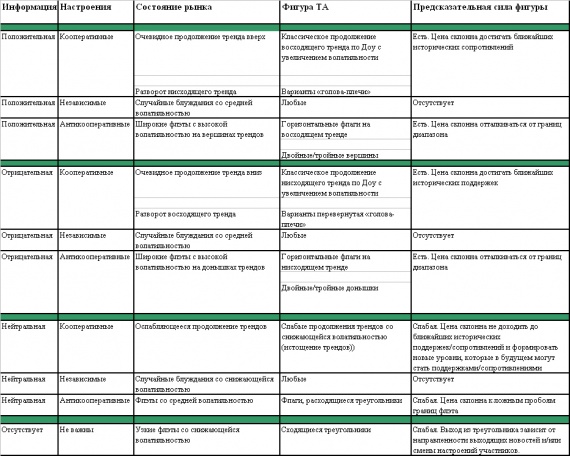
Итак, когда же работают фигуры технического анализа? Мой опыт совмещения различных видов ценового анализа говорит, что они хорошо работают в ситуациях однозначно трактуемого потока информации, поддержанного однозначным (кооперативным или антикооперативным) поведением участников рынка. Такая ситуация существует на рынке примерно в 30-50 % времени.
Если поток информации нейтрален и/или поведение участников рынка независимое, то формирование фигур является событием, близким к случайному и работать так, как описано в книгах они не будут. В этом случае – это типичные «миражи» случайного блуждания. Такая непредсказуемость занимает на рынке 30-40 % времени.
И есть еще 10-20 % ситуаций отсутствия важной информации при любом поведении участников. В этом случае рынок формирует сходящиеся треугольники, выход из которых непредсказуем и зависит исключительно от направленности первой серьезной новости, способной заставить участников рынка активно принимать решения.
Приведенная выше таблица достаточно сложна для практического применения, поскольку требует опыта оценки «качества» информационного потока и умения определять настроения участников рынка, путем вычисления фрактальной размерности. К счастью еще один способ прогнозировать развитие фигуры технического анализа, основанный на одном любопытном эмпирическом факте.
Для начала введем несколько определений. Выделим на графике цены все ценовые экстремумы (видимые глазом максимумы и минимумы) и соединим их прямыми линиями, как показано на рисунке 1.
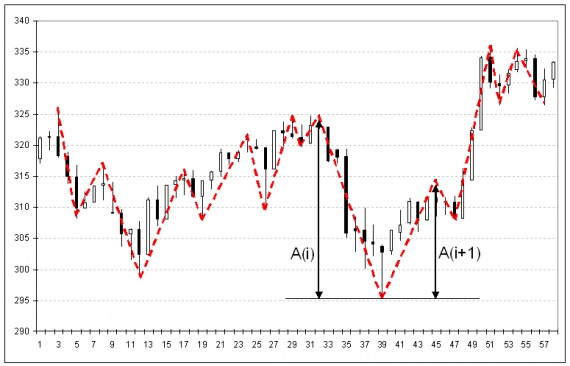
Назовем волной движение цены от локального максимума к следующему за ним локальному минимуму, или наоборот от локального минимума, к следующему за ним локальному максимуму. Тогда ценовое движение можно представить последовательностью волн, каждая из которых направлена в противоположную сторону от предыдущей.
Введем амплитуду волны А, как модуль разности между ценой окончания и ценой начала волны. Волны, амплитуда которых больше амплитуды предыдущей волны будем называть в духе теории Элиотта импульсными, а волны, амплитуда которых меньше либо равна амплитуде предыдущей — корректирующими.
Более строго: Если А(i)>A(i-1), то волна импульсная, если А(i)<=A(i-1), то волна корректирующая. Таким образом, движение цены можно представить последовательностью следующих друг за другом импульсных и корректирующих волн. А теперь, внимание, самое важное! Статистические свойства введенных таким простым способом волн, оказываются практически одинаковыми для большинства финансовых рынков (кроме, может быть, рынка облигаций). И описать эти свойства можно двума простыми фразами. Если предыдущая волна была импульсной, то текущая волна с вероятностью больше 0,5 будет корректирующей. Если предыдущая волна была корректирующей, то текущая волна с вероятностью больше 0,5 будет импульсной. Типичные для большинства рынков диапазоны соответствующих вероятностей представлены в следующей таблице:
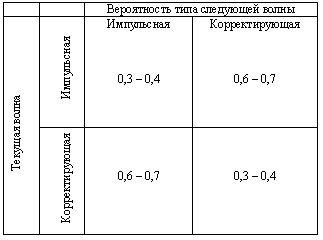
Удивительно, но статистические свойства ценовых движений между локальными экстремумами полностью соответствуют положениям теории Чарльза Доу, который считал, что начавшаяся тенденция имеет больше шансов продолжиться, чем измениться. В соответствии с приведенной таблицей это именно так: если мы наблюдаем импульсную волну вверх, с пробитием предыдущего ценового максимума, то наиболее вероятно, что она сменится коррекцией вниз, а затем снова с большей вероятностью последует импульсное движение вверх!
А что же такое тогда фигуры технического анализа? Оказывается, что это просто различные последовательности из нескольких волн разного типа. Например классическое трендовое движение описывается наиболее вероятной последовательностью импульс-коррекция – импульс – коррекция – импульс. Всевозможные разворотные фигуры –это сбой в одном звене наиболее вероятной последовательности. Например, самая частая разворотная фигура «голова-плечи» может быть описана двумя возможными последовательностями: импульс – коррекция – импульс – коррекция – коррекция – импульс, или импульс – коррекция – импульс – импульс – коррекция – импульс. В первом случае сбой в наиболее вероятной последовательности произошел на пятом шаге, когда вместо более вероятного импульса на рынке возникла корректирующая волна. Во втором случае сбой произошел на четвертом шаге, когда вместо более вероятной коррекции на рынке возникло импульсное движение вниз (соответствующие паттерны изображены на рисунке 2).
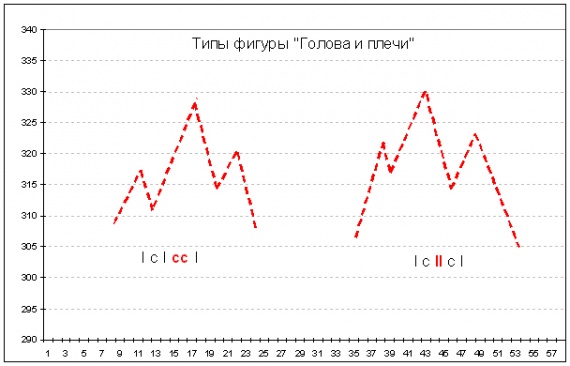
Рисунок 2. Волновые варианты формирования фигуры «голова-плечи».
Различные сходящиеся и расходящиеся треугольники – это многократные сбои в наиболее вероятной последовательности. Сходящийся треугольник описывается формулой коррекция – коррекция – коррекция – коррекция -…, а расходящийся формулой импульс – импульс – импульс – импульс-…
Зная универсальные свойства волн, и немного потренировавшись, можно легко найти волновые формулы всех фигур технического анализа. Но самое важное заключается в том, что наблюдая только график цены и выделяя в нем две последних волны можно быстро прогнозировать наиболее вероятный сценарий развития событий на рынке. Так, например, если наблюдается коррекция восходящей импульсной волны, то до тех пор, пока текущая цена выше основания предыдущего движения более вероятно окончание коррекции и продолжение роста к уже достигнутым ранее максимумам. Если же цена опустилась ниже основания предыдущей импульсной волны, то это явный статистический сигнал разворота и на ближайшей коррекции вверх следует искать возможности для продажи. А выходы из сходящихся треугольников с большей вероятностью происходят в сторону противоположную последнему локальному экстремуму.
Конечно, описанный визуальный анализ является достаточно грубым средством для принятия решений, однако в условиях нехватки времени на детальный анализ текущий ситуации он позволяет быстро и эффективно понять что же может произойти с ценами дальше и наметить тактику торговых действий в случае реализации как более, так и менее вероятного сценария.
В конце девятнадцатого века, примерно в одно и тоже время, появились две совершенно противоположные по смыслу концепции, описывающие поведение цен на фондовом рынке. В 1900-м году Луи Башелье написал диссертацию «теория спекуляций», основанную на наблюдениях за поведением цен облигаций на парижской бирже. За семь лет до Эйнштейна он предложил формальную математическую модель случайного блуждания, в соответствии с которой поведение цен было похоже на поведение броуновской частицы под ударами мелких молекул.
В период с 1890 по 1902 годы Чарльз Доу, первый редактор газеты «Wall Street Journal» и автор самого известного биржевого индекса, написал серию статей, которая позже превратилась в «теорию Доу». Он считал, что поведение цен описывается закономерными тенденциями, или направленными движениями вверх или вниз, которые отражают господствующее на бирже мнение о будущем экономики или отдельной компании. Так началось противостояние двух принципиально противоположных концепций, которое не окончено и по сей день.
Гипотеза Башелье за период с 1930 по 1950-й годы превратилась в гипотезу эффективного рынка, на котором большое количество независимых рациональных участников быстро и правильно принимают решения на основе поступающей информацию. В результате вся имеющаяся на рынке информация оказывается включенной в цену, а поведение цен оказывается случайным блуждание, которое невозможно прогнозировать. Эта теория господствовала в академической теории финансов вплоть до конца двадцатого века.
Теория Доу пришлась больше по нраву трейдерам, реально торгующим на фондовом рынке, поскольку позволяла принимать решения на основе анализа ценовых графиков, что с точки зрения гипотезы эффективного рынка делать бессмысленно – все видимые глазом движения цен являются «причудливой игрой случая», как выпадение красного или черного в рулетке. Однако, практики знали, что это не так, или по крайней мере не совсем так. Уже в тридцатых годах двадцатого века, на основе положений Чарльза Доу была разработана классификация «типичных» вариантов поведения цен, означающих смену или продолжение наблюдаемой рыночной тенденции. Сейчас их называют «фигурами» или паттернами, а обнаружение таких фигур на графиках техническим визуальным анализом. В отличие от индикаторного технического анализа, требующего иногда достаточно сложных расчетов, визуальный анализ весьма прост – для него необходимо только видеть график цены и помнить наиболее важные фигуры.
Между тем даже сегодня фигуры технического анализа остаются одной из наиболее спорных тем. С одной стороны, их видит на графиках практически любой начинающий трейдер. С другой стороны, работа фигур теханализа по правилам, описанных в книгах, вызывает большие сомнения, особенно когда начинается «проверка гармонии алгеброй», т.е. формальные и статистически правильные исследования. Если рассматривать паттерны типа «голова и плечи» и т.д. отвлеченно от рынка, как некие образы, картинки, возникающие в графиках цены, то грамотная статистическая проверка будет неизменно приводить к печальному результату: вероятность срабатывания фигуры по сценарию, описанному в книгах близка к 50 %. Однако, иногда они срабатывают очень даже хорошо. Можно ли отличить ситуацию когда фигура сработает, от обратной? Иногда можно.
Но для того, чтобы ответить на вопрос о срабатывании фигур сначала нужно ответить на более фундаментальный вопрос: что движет рынком?
Один из возможных, достаточно очевидных ответов – решения участников рынка, реализованные в сделках. Почему люди принимают решения? Достаточно очевидный ответ, в духе академической науки — реагируя на информацию. Следовательно, одним из важных факторов движения цен является информация, поступающая на рынок. Ее можно разделить на четыре категории:
Очевидно положительная – такая информация, которая для большинства участников рынка является понятным поводом для покупки.
Очевидно отрицательная – такая, которая для большинства участников является основанием для продажи.
Нейтральная – это весьма частый вид информации (пожалуй, наиболее частый на рынке), когда ее можно интерпретировать и как положительную и как отрицательную. Эта информация вызывает у части участников решения о покупке, а у другой части – решения о продаже.
И наконец, есть еще один вид информации – ее отсутствие. Это периоды на рынке, когда выходящие новости настолько слабы, что не вызывают реакции участников рынка в виде сделок.
Согласно современным представлениям, поступление информации на рынок — процесс близкий к случайному (математики говорят пуассоновский). Да, конечно, бывают периоды, когда одна за другой долго идут положительные или отрицательные новости, но такие периоды редки. Поэтому, если бы движение определялось только информацией, то цены были бы в точности случайным блужданием, как это и предполагает гипотеза эффективного рынка.
Однако, есть еще один фактор, который на сегодня можно считать доказанным и который вносит коррективы в движение цен. Это настроения участников рынка, определяющие их отношение к информации. Численным выразителем настроений участников может быть фрактальная размерность графика цены, или является знаменитый показатель Херста H, связанный с фрактальной размерностью соотношением D=2-H. Его значение задает три возможных типа поведения участников рынка, которые можно описать так.
При H>0.5 настроения «кооперативны» и участники склонны одинаково оценивать выходящие новости. В первом приближении значение Н задает вероятность, с которой участники принимают одинаковые решения на основе выходящей информации. Такое состояние обычно связывается с трендами, поскольку движение цены вверх (вниз) вызывает еще большее желание рыночной толпы покупать (продавать) акции.
Если Н близко к 0.5, то участники рынка склонны действовать независимо друг от друга, независимо оценивать информацию и независимо принимать решения. Поведение цены в данном случае — это классическое случайное блуждание.
При Н<0.5, то участники рынка склонны к антикооперативному поведению. Грубо говоря, они склонны трактовать выходящие новости и движения цен «наоборот». В таком состоянии движение цены вверх вызывает желание продавать акции, а вниз – наборот покупать их. Такое поведение характерно для флэтов.
Таким образом, четыре типа информации три типа поведения участников задают нам все встречающие рыночные ситуации. Поведение цен в этих ситуациях склонно к формированию неких «типичных» паттернов, которые являются отражением преобладающей на рынке информации и характера реакции участников рынка на эту информацию. Вот эти типичные паттерны поведения цен в различных информационно-настроенческих ситуациях с моей точки зрения и составляют набор фигур технического анализа:

Итак, когда же работают фигуры технического анализа? Мой опыт совмещения различных видов ценового анализа говорит, что они хорошо работают в ситуациях однозначно трактуемого потока информации, поддержанного однозначным (кооперативным или антикооперативным) поведением участников рынка. Такая ситуация существует на рынке примерно в 30-50 % времени.
Если поток информации нейтрален и/или поведение участников рынка независимое, то формирование фигур является событием, близким к случайному и работать так, как описано в книгах они не будут. В этом случае – это типичные «миражи» случайного блуждания. Такая непредсказуемость занимает на рынке 30-40 % времени.
И есть еще 10-20 % ситуаций отсутствия важной информации при любом поведении участников. В этом случае рынок формирует сходящиеся треугольники, выход из которых непредсказуем и зависит исключительно от направленности первой серьезной новости, способной заставить участников рынка активно принимать решения.
Приведенная выше таблица достаточно сложна для практического применения, поскольку требует опыта оценки «качества» информационного потока и умения определять настроения участников рынка, путем вычисления фрактальной размерности. К счастью еще один способ прогнозировать развитие фигуры технического анализа, основанный на одном любопытном эмпирическом факте.
Для начала введем несколько определений. Выделим на графике цены все ценовые экстремумы (видимые глазом максимумы и минимумы) и соединим их прямыми линиями, как показано на рисунке 1.

Назовем волной движение цены от локального максимума к следующему за ним локальному минимуму, или наоборот от локального минимума, к следующему за ним локальному максимуму. Тогда ценовое движение можно представить последовательностью волн, каждая из которых направлена в противоположную сторону от предыдущей.
Введем амплитуду волны А, как модуль разности между ценой окончания и ценой начала волны. Волны, амплитуда которых больше амплитуды предыдущей волны будем называть в духе теории Элиотта импульсными, а волны, амплитуда которых меньше либо равна амплитуде предыдущей — корректирующими.
Более строго: Если А(i)>A(i-1), то волна импульсная, если А(i)<=A(i-1), то волна корректирующая. Таким образом, движение цены можно представить последовательностью следующих друг за другом импульсных и корректирующих волн. А теперь, внимание, самое важное! Статистические свойства введенных таким простым способом волн, оказываются практически одинаковыми для большинства финансовых рынков (кроме, может быть, рынка облигаций). И описать эти свойства можно двума простыми фразами. Если предыдущая волна была импульсной, то текущая волна с вероятностью больше 0,5 будет корректирующей. Если предыдущая волна была корректирующей, то текущая волна с вероятностью больше 0,5 будет импульсной. Типичные для большинства рынков диапазоны соответствующих вероятностей представлены в следующей таблице:

Удивительно, но статистические свойства ценовых движений между локальными экстремумами полностью соответствуют положениям теории Чарльза Доу, который считал, что начавшаяся тенденция имеет больше шансов продолжиться, чем измениться. В соответствии с приведенной таблицей это именно так: если мы наблюдаем импульсную волну вверх, с пробитием предыдущего ценового максимума, то наиболее вероятно, что она сменится коррекцией вниз, а затем снова с большей вероятностью последует импульсное движение вверх!
А что же такое тогда фигуры технического анализа? Оказывается, что это просто различные последовательности из нескольких волн разного типа. Например классическое трендовое движение описывается наиболее вероятной последовательностью импульс-коррекция – импульс – коррекция – импульс. Всевозможные разворотные фигуры –это сбой в одном звене наиболее вероятной последовательности. Например, самая частая разворотная фигура «голова-плечи» может быть описана двумя возможными последовательностями: импульс – коррекция – импульс – коррекция – коррекция – импульс, или импульс – коррекция – импульс – импульс – коррекция – импульс. В первом случае сбой в наиболее вероятной последовательности произошел на пятом шаге, когда вместо более вероятного импульса на рынке возникла корректирующая волна. Во втором случае сбой произошел на четвертом шаге, когда вместо более вероятной коррекции на рынке возникло импульсное движение вниз (соответствующие паттерны изображены на рисунке 2).

Рисунок 2. Волновые варианты формирования фигуры «голова-плечи».
Различные сходящиеся и расходящиеся треугольники – это многократные сбои в наиболее вероятной последовательности. Сходящийся треугольник описывается формулой коррекция – коррекция – коррекция – коррекция -…, а расходящийся формулой импульс – импульс – импульс – импульс-…
Зная универсальные свойства волн, и немного потренировавшись, можно легко найти волновые формулы всех фигур технического анализа. Но самое важное заключается в том, что наблюдая только график цены и выделяя в нем две последних волны можно быстро прогнозировать наиболее вероятный сценарий развития событий на рынке. Так, например, если наблюдается коррекция восходящей импульсной волны, то до тех пор, пока текущая цена выше основания предыдущего движения более вероятно окончание коррекции и продолжение роста к уже достигнутым ранее максимумам. Если же цена опустилась ниже основания предыдущей импульсной волны, то это явный статистический сигнал разворота и на ближайшей коррекции вверх следует искать возможности для продажи. А выходы из сходящихся треугольников с большей вероятностью происходят в сторону противоположную последнему локальному экстремуму.
Конечно, описанный визуальный анализ является достаточно грубым средством для принятия решений, однако в условиях нехватки времени на детальный анализ текущий ситуации он позволяет быстро и эффективно понять что же может произойти с ценами дальше и наметить тактику торговых действий в случае реализации как более, так и менее вероятного сценария.
Фрактальный индикатор силы рынка
В связи с тем, что комон самоубился и оживляться, похоже не собирается, да еще грозится похоронить под собой многочисленный контент начну постепенно перетаскивать сюда свои блоги, которые могут оказаться полезными.
Начну с индикатора силы рынка, на котором, собственно построен сейчас фрактальный барометр.
Фрактальный индикатор силы рынка
Для принятия решений об операциях на реальном счете я использую фрактальный индикатор силы рынка. Конечную формулу в этой публикации я выписывать не буду, поскольку она «трехэтажная», да и методика еще не закончена в том виде, в котором мне мы бы хотелось. Здесь будут описаны основные ход мысли, использованный при построении, принципы построения и свойства индикатора. При некотором достаточно небольшом усилии получить аналогичные результаты может любой желающий, знакомый с фракталами не по книгам Вильямса.
1. Основой индикатора является фрактальная размерность графика цены. Что она показывает? Математические ответы типа «изрезанности графика» оказываются неудовлетворительными. Необходимо было найти некую «физическую» интерпретацию, объяснявшую свойства фрактальной размерности, связанные с динамикой цены. Эти свойства я многократно описывал в различных блогах, поэтому здесь не буду подробно на них останавливаться.
После достаточно долгих поисков, была найдена интерпретация (еще не окончательная, но рабочая), которая заключается в следующем. Если мы вычтем из размерности графика единицу, то получим показатель, который изменяется от 0 до 1. Он называется индексом фрактальности. Предположительно, этот индикатор отражает долю преобладающей группы (покупателей и продавцов, или быков и медведей) на интервале расчета показателя.
Так, если индекс фрактальности меньше 0,5, например равен 0,3, то это означает, что:
Доля быков равна Bulls=0,7 в случае роста цены на интервале расчета.
Доля быков равна Bulls=0,3 в случае снижения цены на интервале расчета.
Если индекс фрактальности больше 0,5, например равен 0,6, то это означает что:
Доля быков равна Bulls=0,6 в случае роста цены на интервале расчета.
Доля быков равна Bulls=0,4 в случае снижения цены на интервале расчета.
Если индекс фрактальности равен 0,5, то доли быков и медведей на интервале примерно равны.
Доля медведей, соответственно, связана с долей быков очевидным соотношением: Bears=1-Bulls
2. Предположим довольно естественное свойство психологической инерции участников рынка. Оно означает, что в среднем участники рынка не меняют своего настроения резко (кроме некоторых особых случаев, которые достаточно редки). Покупатель, в будушем скорее останется покупателем, а продавец – продавцом. Тогда можно предположить, что доли быков и медведей в ближайшем будущем будут пропорциональны уже имеющимся долям:
Bulls(i+1)=a*Bulls(i)
Bears(i+1)=b*Bears(i)
Uгде а и bнекоторые константы. Вопрос определения этих констант один из самых сложных и тонких в этом индикаторе. Ниже я опишу и другие способы, которые будут исследованы в ближайшем будущем. В текущей версии индиктора эти константы определяются из следующего предположения. Покупать в текущей точке готовы те трейдеры, которые ранее купили ниже текущей цены, а продавать те, которые продали ранее выше текущей цены. Тогда коэффициенты можно определить из следующих отношений:
a=(C(i)-L(i))/(H(i)-L(i)), b=1-a.
Я вовсе не уверен, что это лучший вариант определения этих коэффициентов, но это пока лучший из испробованных вариантов по свойствам.
Соответственно, текущая сила рынка для данного масштаба расчета равна
F(i)= a*Bulls(i)-b*Bears(i).
3. На рынке существуют разные группы участников, различающиеся по объемы средств от мелких спекулянтов до глобальных фондов. Чем больше средств у участника рынка, тем больше временной масштаб его операций. Мелкие спекулянты действуют в основном на внутридневных масштабах, глобальные фонды на месячных и квартальных. Соответственно сила быков и медведей возрастает при увеличении масштаба операций. Для определения итогового индикатора силы нужно использовать несколько масштабов. Соответственно, в текущей версии итоговый индикатор использует четыре масштаба:
F=F1*(t1^c)+ F2*(t2^c)+ F3*(t3^c)+ F4*(t4^c).
Масштабы t1, t2, t3 и t4 равны 2,4,8 и 16 свечей соответственно, а константа с=1/2
Свойства индикатора.
График индикатора выглядит примерно так (расчет по дневным данным индекса РТС):
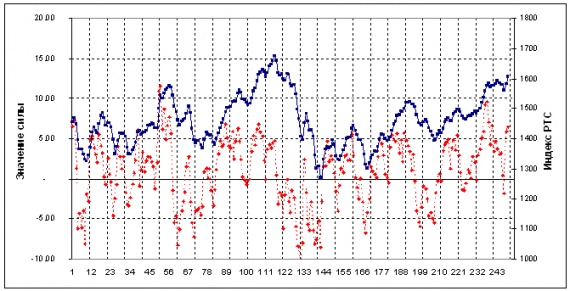
Синяя кривая – среднедневное значение индекса РТС, красная – значение индикатора силы. Нахождение индикатора в положительной зоне соответствует участкам трендов вверх, в отрицательной – участкам трендов вниз.
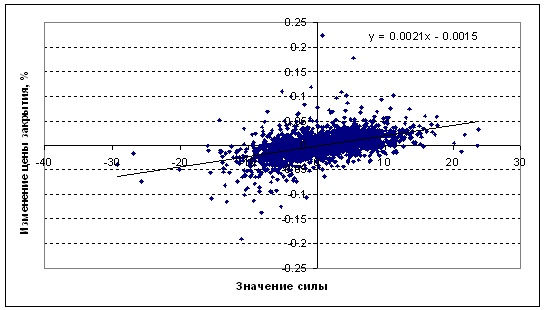
При этом, оказывается, что приращения цен закрытия оказываются чаще положительными, если индикатор находится в положительной области и отрицательными, если индикатор, соответственно в отрицательной зоне:
Достаточно важным свойством индикатора оказывается сохранение положения. С вероятностью около 80 – 85 % индикатор будет оставаться в той зоне, где находился до этого. Это означает, что смена знака индикатора является важным сигналом смены преобладающей группы и соответственно динамики цены. Если индикатор стал положительным, то это сигнал на покупку, отрицательным – на продажу.
Есть еще один тип сигналов, т.н. дивергенции. Рост индикатора в отрицательной зоне при снижении цены часто дает прогноз локального минимума, а снижение индикатора в положительной зоне при росте цены часто означает торможение роста.
Самый простой способ торговли – удержание позиций в соответствии со знаком индикатора. При положительном значение – лонгов, при отрицательном –шортов или денег. График торговой стратегии по таким правилам для индекса РТС и приводить не буду, он слишком оптимистичен. Приведу две более осторожных стратегии. Лонговая стратегия покупает индекс при переходе индикатора в положительную зону, а закрывает позицию при первом снижении индикатора в положительной зоне. Шортовая стратегия открывает позицию при переходе индикатора в отрицательную зону, а закрывает ее при первом повышении индикатора в отрицательной зоне:
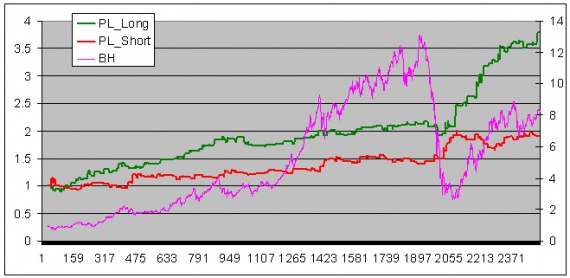
Левая шкала – доходность соответствующих стратегий, правая шкала – доходность индекса РТС.
По отдельным акциям получаются похожие результаты.
Способы модификации индикатора, которые будут исследованы в обозримом будущем (блондинкам не читать!).
Имеет смысл исследовать более сложную зависимость силы от текущих долей быков и медведей. Простейший вариант модификации описается на логистическое отображение, которое, в частности, описывает динамику замкнутых популяций:
Bulls(i+1)=a*(Bulls(i)-Bulls(i)^2).
В такой записи предполагается, что количество быков на следующем шаге увеличивается пропорционально имеющемуся количеству и уменьшается пропорционально квадрату имеющегося количества.
Динамика популяций, описываемая логистическим отображением, имеет весьма нетривиальные свойства в зависимости от значения коэффициента а. Можно полагать, что некоторые из этих свойств имеют место и на фондовом рынке
2. Способ определения коэффициентов а и b. К этому вопросу можно подойти классическим эконометрическим подходом, т.е. определять коэффициенты из двухфакторной регрессионной модели:
C(i)-C(i-1)= a*Bulls(i)-b*Bears(i)+e, где е – нормально распределенная ошибка.
При таком способе коэффициенты будет адаптивно переменными, однако мне не нравится неопределенность, которая будет вноситься выбором длительности ряда, для определения коэффициентов.
Во… Теперь хоть в барометре можно ссылаться не на «вражеский» блог!
Начну с индикатора силы рынка, на котором, собственно построен сейчас фрактальный барометр.
Фрактальный индикатор силы рынка
Для принятия решений об операциях на реальном счете я использую фрактальный индикатор силы рынка. Конечную формулу в этой публикации я выписывать не буду, поскольку она «трехэтажная», да и методика еще не закончена в том виде, в котором мне мы бы хотелось. Здесь будут описаны основные ход мысли, использованный при построении, принципы построения и свойства индикатора. При некотором достаточно небольшом усилии получить аналогичные результаты может любой желающий, знакомый с фракталами не по книгам Вильямса.
1. Основой индикатора является фрактальная размерность графика цены. Что она показывает? Математические ответы типа «изрезанности графика» оказываются неудовлетворительными. Необходимо было найти некую «физическую» интерпретацию, объяснявшую свойства фрактальной размерности, связанные с динамикой цены. Эти свойства я многократно описывал в различных блогах, поэтому здесь не буду подробно на них останавливаться.
После достаточно долгих поисков, была найдена интерпретация (еще не окончательная, но рабочая), которая заключается в следующем. Если мы вычтем из размерности графика единицу, то получим показатель, который изменяется от 0 до 1. Он называется индексом фрактальности. Предположительно, этот индикатор отражает долю преобладающей группы (покупателей и продавцов, или быков и медведей) на интервале расчета показателя.
Так, если индекс фрактальности меньше 0,5, например равен 0,3, то это означает, что:
Доля быков равна Bulls=0,7 в случае роста цены на интервале расчета.
Доля быков равна Bulls=0,3 в случае снижения цены на интервале расчета.
Если индекс фрактальности больше 0,5, например равен 0,6, то это означает что:
Доля быков равна Bulls=0,6 в случае роста цены на интервале расчета.
Доля быков равна Bulls=0,4 в случае снижения цены на интервале расчета.
Если индекс фрактальности равен 0,5, то доли быков и медведей на интервале примерно равны.
Доля медведей, соответственно, связана с долей быков очевидным соотношением: Bears=1-Bulls
2. Предположим довольно естественное свойство психологической инерции участников рынка. Оно означает, что в среднем участники рынка не меняют своего настроения резко (кроме некоторых особых случаев, которые достаточно редки). Покупатель, в будушем скорее останется покупателем, а продавец – продавцом. Тогда можно предположить, что доли быков и медведей в ближайшем будущем будут пропорциональны уже имеющимся долям:
Bulls(i+1)=a*Bulls(i)
Bears(i+1)=b*Bears(i)
Uгде а и bнекоторые константы. Вопрос определения этих констант один из самых сложных и тонких в этом индикаторе. Ниже я опишу и другие способы, которые будут исследованы в ближайшем будущем. В текущей версии индиктора эти константы определяются из следующего предположения. Покупать в текущей точке готовы те трейдеры, которые ранее купили ниже текущей цены, а продавать те, которые продали ранее выше текущей цены. Тогда коэффициенты можно определить из следующих отношений:
a=(C(i)-L(i))/(H(i)-L(i)), b=1-a.
Я вовсе не уверен, что это лучший вариант определения этих коэффициентов, но это пока лучший из испробованных вариантов по свойствам.
Соответственно, текущая сила рынка для данного масштаба расчета равна
F(i)= a*Bulls(i)-b*Bears(i).
3. На рынке существуют разные группы участников, различающиеся по объемы средств от мелких спекулянтов до глобальных фондов. Чем больше средств у участника рынка, тем больше временной масштаб его операций. Мелкие спекулянты действуют в основном на внутридневных масштабах, глобальные фонды на месячных и квартальных. Соответственно сила быков и медведей возрастает при увеличении масштаба операций. Для определения итогового индикатора силы нужно использовать несколько масштабов. Соответственно, в текущей версии итоговый индикатор использует четыре масштаба:
F=F1*(t1^c)+ F2*(t2^c)+ F3*(t3^c)+ F4*(t4^c).
Масштабы t1, t2, t3 и t4 равны 2,4,8 и 16 свечей соответственно, а константа с=1/2
Свойства индикатора.
График индикатора выглядит примерно так (расчет по дневным данным индекса РТС):

Синяя кривая – среднедневное значение индекса РТС, красная – значение индикатора силы. Нахождение индикатора в положительной зоне соответствует участкам трендов вверх, в отрицательной – участкам трендов вниз.
При этом, оказывается, что приращения цен закрытия оказываются чаще положительными, если индикатор находится в положительной области и отрицательными, если индикатор, соответственно в отрицательной зоне:

Достаточно важным свойством индикатора оказывается сохранение положения. С вероятностью около 80 – 85 % индикатор будет оставаться в той зоне, где находился до этого. Это означает, что смена знака индикатора является важным сигналом смены преобладающей группы и соответственно динамики цены. Если индикатор стал положительным, то это сигнал на покупку, отрицательным – на продажу.
Есть еще один тип сигналов, т.н. дивергенции. Рост индикатора в отрицательной зоне при снижении цены часто дает прогноз локального минимума, а снижение индикатора в положительной зоне при росте цены часто означает торможение роста.
Самый простой способ торговли – удержание позиций в соответствии со знаком индикатора. При положительном значение – лонгов, при отрицательном –шортов или денег. График торговой стратегии по таким правилам для индекса РТС и приводить не буду, он слишком оптимистичен. Приведу две более осторожных стратегии. Лонговая стратегия покупает индекс при переходе индикатора в положительную зону, а закрывает позицию при первом снижении индикатора в положительной зоне. Шортовая стратегия открывает позицию при переходе индикатора в отрицательную зону, а закрывает ее при первом повышении индикатора в отрицательной зоне:

Левая шкала – доходность соответствующих стратегий, правая шкала – доходность индекса РТС.
По отдельным акциям получаются похожие результаты.
Способы модификации индикатора, которые будут исследованы в обозримом будущем (блондинкам не читать!).
Имеет смысл исследовать более сложную зависимость силы от текущих долей быков и медведей. Простейший вариант модификации описается на логистическое отображение, которое, в частности, описывает динамику замкнутых популяций:
Bulls(i+1)=a*(Bulls(i)-Bulls(i)^2).
В такой записи предполагается, что количество быков на следующем шаге увеличивается пропорционально имеющемуся количеству и уменьшается пропорционально квадрату имеющегося количества.
Динамика популяций, описываемая логистическим отображением, имеет весьма нетривиальные свойства в зависимости от значения коэффициента а. Можно полагать, что некоторые из этих свойств имеют место и на фондовом рынке
2. Способ определения коэффициентов а и b. К этому вопросу можно подойти классическим эконометрическим подходом, т.е. определять коэффициенты из двухфакторной регрессионной модели:
C(i)-C(i-1)= a*Bulls(i)-b*Bears(i)+e, где е – нормально распределенная ошибка.
При таком способе коэффициенты будет адаптивно переменными, однако мне не нравится неопределенность, которая будет вноситься выбором длительности ряда, для определения коэффициентов.
Во… Теперь хоть в барометре можно ссылаться не на «вражеский» блог!
